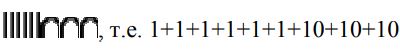Цифры и буквы в человеческом сознании |
Эволюция знаков письменности и чисел с семиотической точки зрения
Принципиальное отличие Homo sapiens – Человека разумного
– от всех других известных живых существ состоит в наличии у него сознания. Один
из основоположников семиотики Чарльз Моррис однажды справедливо отметил: «Человеческая
цивилизация невозможна без знаков и знаковых систем, человеческий разум неотделим
от функционирования знаков, – а возможно, и вообще интеллект следует отождествить
именно с функционированием знаков» (Моррис, 1983, с. 37–38). Переход от иконических
знаков и знаков-индексов к условным знакам (символам) является, на наш взгляд, важнейшим
показателем развития абстрактного мышления. И этот переход хорошо прослеживается
в истории письма и знаков чисел (цифр). Осознание роли знаков в человеческой культуре
привело к бурному развитию семиотики в ХХ в. Весьма многозначительным явлением,
говорящим о возрастающей роли знаков, выглядит и все более широкое распространение
в конце ХХ – начале ХХI в. симулякров – знаков, оторвавшихся от своей исходной почвы,
утративших свое значение в действительном мире и относящихся только к ментальным
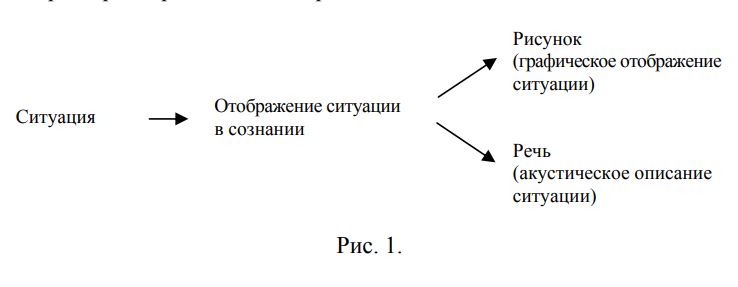
конструкциям. Знак – это единство означающего и означаемого. Но если означаемым может быть и реально существующий объект, и воображаемый, то означающим – лишь чувственно воспринимаемый. В истории цивилизации особую роль сыграло возникновение и широкое использование знаков акустических, воспринимаемых на слух, и графических, воспринимаемых визуально. Порядка 80% информации о внешнем мире человек получает через зрение, через слух – значительно меньше, но именно со слухом связано восприятие речи, а значит, и языка, что делает этот тип знаков необычайно важным. Акустически и визуально воспринимаемые знаки часто дополняют друг друга. Так, зрительно воспринимаемые жесты, позы, выражения лица и т.п. выступают как паралингвистические факторы, дополняющие речь, хотя и не играют в ней решающую роль. Эти знаки можно до определенной степени считать естественными (по классификации Ч. Пирса – знаками-индексами[1]), связанными с физиологией человека, хотя по мере развития культуры многие из них несут на себе все больший отпечаток условности и связаны с воспитанием в определенной среде (например, жестикуляция). Но еще более важными среди всех визуально воспринимаемых знаков являются искусственные, созданные самим человеком графические знаки, и прежде всего знаки письменности и чисел. И хотя они служат для разных целей, связаны с различными интеллектуальными операциями, их эволюция обнаруживает много общего. Главную тенденцию их развития с точки зрения семиотики можно выразить одной фразой: оно шло от иконических знаков к условным. Ниже мы попробуем проследить основные этапы развития письменности и числовых обозначений (цифр). ПисьменностьЭволюция письменности в
настоящее время хорошо изучена в лингвистике. Отвлекаясь от конкретно-исторических
особенностей развития письменности и фиксируя лишь общую логику развития, в истории
письменности можно выделить следующие этапы: пиктография – иероглифика – силлабическое
(слоговое) письмо – алфавитное письмо. Исходной предпосылкой письменности были рисунки,
древнейшие из них относятся к периоду раннего палеолита. Самые древние рисунки
– изображения отдельных объектов (чаще всего – различных животных), обладавшие высокой
степенью реализма, а значит, и иконичности. Шагом на пути к письменности стало создание
композиций, что позволило отображать уже
не только отдельные объекты, но и некоторую ситуацию,
в которой они находятся, или событие,
происходящее с ними. Такая композиция могла включать изображения как одушевленных
объектов (люди и животные с их позами и жестами), так и неодушевленных (оружие,
элементы пейзажа и т.п.). Появление композиций в истории первобытной живописи сопровождалось
в целом уменьшением степени реализма изображений, их схематизацией (являясь явным
свидетельством развития абстрактного мышления), что и вело к появлению пиктографов.
Пиктографию часто называют рисуночным или образным письмом,
хотя точнее ее назвать протописьменностью. Большинство изображений в ней (при всей
их схематизации) сохраняют еще иконический характер, хотя встречаются и условные
знаки (символы), происходящие от иконических, но такие, где означающее уже утратило
заметное сходство с означаемым. Появление пиктографии обычно относят к эпохе позднего
палеолита или мезолита. И если рисунок отдельного объекта можно рассматривать в
качестве графического «протоимени», то композиция в целом уже выступает в роли
«протовысказывания». Каждая отдельная композиция (как и фотография) отображает
лишь некий «мгновенный срез» событий, и в этом смысле такое «протовысказывание»
задает некое неопределенное настоящее время. Рисунок всегда двумерен (а при наличии
перспективы – иллюзорно становится трехмерным) и передает только пространственные
измерения. Но любое развитие событий имеет временное измерение, что не может быть
отображено на одном рисунке[2].
Революционный характер пиктографии мы видим как раз в том, что в ней появляется
последовательность композиций, позволяющая
отображать последовательность событий,
составляя «прототекст». Такого рода «прототекст», как и кинематограф на ранних этапах
его существования, состоял из отдельных «протовысказываний»«кадров», и его тоже
можно назвать «Великим немым». Поскольку в большинстве случаев рисунки еще похожи
на обозначаемые объекты (чисто условные знаки встречаются реже), такого рода «прототекст»
универсален и в принципе может пониматься носителями любых национальных языков.
Правда, степень понимания его остается неопределенной, так как не известен точный
смысл, который «авторы» вкладывали в этот «текст»: поэтому относительно большинства
известных пиктографов современные исследователи всегда предлагают целый ряд различных
интерпретаций. Данное протописьмо совершенно не связано со звучанием речи, а общая связь такого «прототекста»
с речью и языком весьма опосредованна, хотя ее и нельзя полностью игнорировать.
Во-первых, выбор определенного сюжета для изображения, как и вкладываемого в него
смысла, определяется сознанием, работа которого, как и общее развитие, непосредственно
связана с языком. При этом связь сознания с рисунком имеет еще один важный аспект:
в отличие от фотографии, рисунок передает не действительность как таковую, а тот
образ действительности, который сложился
в сознании, неся отпечаток как субъективного, так и интерсубъективного опыта художника.
Во-вторых, серия рисунков, передающая последовательностьсобытий в действительности, а значит, и отображающая временное измерение в пространственном,
тем самым обретает и определенное сходство с речью, имеющей линейный характер во
временном измерении.
Графическое (пиктографическое) и акустическое (речевое) отображения ситуации выступают здесь как два параллельных процесса. Древнейшей формой собственно письменности стало иероглифическое
письмо, возникшее на базе пиктографии. Термин «иероглифика» греческого происхождения
и относился к египетской письменности, в буквальном переводе он означает «священные
письменные знаки», тогда как сами египтяне называли свое письмо «священной речью».
Здесь во-первых, важно отношение к письменности как к чему-то священному, полученному
от бога (аналогичные воззрения на происхождение письменности имелись и у всех других
народов древности); а во-вторых, особый интерес представляет тот факт, что египтяне
отождествляли запись речи с самой речью. Вопрос о связи письменного текста
с речью представляет, с нашей точки зрения, особый интерес, и мы будем еще обращаться
к нему ниже. В эволюции иероглифического письма выделим два момента.
Во-первых, она вела к стандартизации в начертании графических знаков, и иероглиф
(в отличие от пиктографа) есть не произвольный, сколь угодно точный или, напротив,
схематичный рисунок некоторого объекта, а именно определенный графический знак,или, точнее, означающее в составе знака.Сохраняя свою иконическую природу в плане сходства с означаемым, такой рисунок приобретает
ряд свойств условного знака: распознается именно как знак из системы письменных знаков, получает в данной
системе несколько различных, но фиксированных значений (обычно из одного семантического
гнезда, например рисунок ног может означать не только сами ноги, но ряд действий,
связанных с ними, например ходьбу, движение в целом и т.д.), при этом на выбор его
конкретного значения в каждом случае влияет контекст его использования. Во-вторых,
эволюция письменности вела к упрощению, схематизации начертания знаков, так что
со временем многие иероглифы вообще утрачивали очевидное сходство с означаемым,
трансформируясь из иконических в чисто условные знаки, значение которых надо было
специально изучать и запоминать писцам. Условный характер неизбежно получали и все
более многочисленные в развивающейся письменности знаки для обозначения ряда действий,
а также оценок, эмоций и желаний людей и т.п., которые довольно трудно (если вообще
возможно) отобразить в рисунке, сюда же надо добавить и появляющиеся знаки для ряда
абстрактных понятий, которыми уже активно оперировало человеческое мышление на этом
этапе развития, а также особые знаки – носители чисто языковых функций. Письменный текст, представляющий собой последовательность графических знаков, как
и речь с ее акустическими знаками, имеет линейный характер, и его пространственное
расположение (по горизонтали и / или вертикали) коррелирует с протяженностью речи
во времени. И если в пиктографии первична связь последовательности рисунков с последовательностью
событий, то в иероглифическом письме усиливается связь именно с последовательностью
речи, описывающей события: несколько записанных
предложений могут говорить о различных составляющих одного и того же события, которые
в рисунке были бы отражены сразу, или о разных событиях, происходящих в один и тот
же момент времени, что в принципе невозможно отобразить на одном рисунке. А с появлением
специальных знаков, указывающих на время (например, грамматических форм глаголов),
более позднее предложение может говорить о более ранних событиях и т.п. Принципиальное отличие иероглифики от пиктографии (благодаря чему пиктография была лишь протописьмом, а иероглифика – это уже письменность как таковая) состоит в том, что это именно запись речи, описывающей ситуацию, но такая запись, где в качестве имен объектов все еще выступают их изображения-подобия (рис. 2).
Следующей стадией развития письма было слоговое (силлабическое) – первая форма фонетического письма. Его появление можно считать очередной революцией в развитии письменности, поскольку теперь в тексте вместо изображения означаемого имеет место фиксация звучания данного имени в речи. В качестве знаков слогов первоначально могли использоваться любые иероглифы, обозначавшие объекты, первый слог имен (обычно – согласная + гласная или только гласные) которых звучал так же, как в фиксируемом имени (например, в современном русском языке слово «ко-ро-ва» мы могли бы задать как «комар», «рога», «ваза» или как «ковер», «рогожа» и «варан», и т.п.). Затем начертание знаков стандартизировалось (каждый слог стал обозначаться только определенным знаком), упрощалось, схематизировалось – шел процесс усиления их условного характера. Более сложный характер записи имен объектов при таком подходе (вместо одного иероглифа – несколько знаков слогов) вполне компенсировался тем, что количество исходных знаков, которые надо было заучивать, резко сокращалось: вместо десятков тысяч иероглифов – порядка 100200 знаков слогов. Такое письмо имеет гораздо более тесную связь с языком и речью и обладает значительно возросшими выразительными способностями в плане передачи мысли, выраженной в речи, причем особенно революционными – для передачи рассуждений об абстрактных объектах, а также позволяет передавать ряд грамматических особенностей конкретного национального языка. Однако для прочтения такого текста уже необходимо знание языка, на котором он написан.
Интересно отметить, что в финикийском алфавите каждая
буква получила особое название – им было
определенное слово, начинавшееся с того же звука; так, первая буква называлась
«алеф» («бык»), вторая – «бет» («дом»), третья – «гимель» («верблюд») и т.д.[3]По одной из гипотез, начертание данной буквы возникло в результате трансформации
иероглифа, обозначавшего соответствующий объект. Таким образом, акрофоническая мнемоника пришла на смену
исходному подобию изображения и изображаемого. (Наличие имен для букв облегчало
их запоминание, но одновременно это можно рассматривать и как напоминание об исходном
происхождении этих букв от рисунков, хотя не обязательно, что это было связано с
реальным происхождением данных знаков именно от этих изображений.) Когда греки начали
использовать этот алфавит, названия букв несколько изменились в соответствии с греческой
фонологией («алеф» – «альфа», «бет» – «бета», «гимель» – «гамма» и т.д.), и имена
букв стали бессмысленными, превратившись в чисто условные знаки. Позднее, с добавлением
или изменением некоторых букв в древнегреческом алфавите, некоторые получили осмысленные
названия; так, «омикрон» и «омега» соответственно значат «маленькое о» и «большое
о». Буквы обозначают звуки, не обладая никаким внешним сходством
с означаемым и тем более с объектами, обозначаемыми словами, состоящими из соответствующих
звуков, а значит, буквы являются чисто условными знаками, полностью утратившими
исходную иконичность первых графических знаков-рисунков. Фонетическая письменность
непосредственно связана с национальными языками и способна максимально точно передавать
звучание речи. Впрочем, условный характер начертания букв позволяет их использовать
для обозначения сходных, но далеко не тождественных звуков (фонем) в различных языках.
Так, в основе письменности всех европейских народов лежат два варианта (западный
и восточный) одной и той же древнегреческой письменности. Таким образом, общий путь развития письменности можно
охарактеризовать как путь от иконических знаков к условным, от изображения объектов в некоторой ситуации– к фиксации высказываний о ситуации.
Отметим еще один интересный факт: в тех цивилизациях,
где сформировалась развитая письменность (уже на уровне иероглифики), обычно возникал
и особый «литературный язык», отличающийся от разговорного как набором лексики,
так и определенным отбором грамматических норм. В мистических учениях, связанных с письменностью и языком,
нашли свое отражение некоторые стадии развития письма. Так, в каббале существовал
метод «нотарикон», по которому имена ангелов из Торы считались чем-то вроде аббревиатур,
которые пытались расшифровать. Обращаясь к истории письменности, можно с удивлением
обнаружить, что, действительно, любая запись слова алфавитным письмом в идеале может
быть «реконструирована»: сначала путем возвращения к слогам (на базе которых возникли
буквы), а затем и к тем иероглифам, из которых образовались знаки слогов, а значит,
и стоящими за ними понятиями. Отметим также, что вплоть до Нового времени во многих районах мира (Греция, Индия, Китай, арабские страны, средневековая Европа и т.д.) широко была распространена так называемая «естественная» теория языка, по которой имя объекта (по крайней мере на «истинном языке») непосредственно связано с сущностью означаемого. Имя, как и изображение объекта в рисунке, считалось подобием человека[4]. Соответственно, и объекты, называющиеся сходными именами, считались также внутренне сходными, сохраняя древнейшие представления о магии подобия и законе партиципации, сформулированном Л. Леви-Брюлем (Леви-Брюль, 1994). Эти представления в сознании людей порождали мистическую связь (рис. 4).
Интересный пример таких магических представлений дают древнеегипетские тексты, где частичное или полное совпадение написания различных слов трактуется как определенная связь внеязыковых действий и объектов. Так, в «Драматическом папирусе из Ремессеума» Хор, обращаясь к «сыновьям Хора», говорит: Сделайте так, чтобы Сет вечно пребывал (джед)
ниже Осириса. Но слово «джед», кроме значения «вечно пребывать», имеет еще значение «столб». И тогда утверждение о том, что посланцы фараона установили столб, оказывается равнозначным выполнению соответствующего указания Хора. В (Ассман, 1999) приводится еще целый ряд аналогичных примеров. ЦифрыОбратимся теперь к истории знаков
чисел. Считать люди начали задолго до появления письменности, уже к периоду палеолита
относится ряд находок, на которых, по-видимому, зафиксированы числа с помощью зарубок,
точек и других однотипных знаков. Однако история формирования систем знаков для
обозначения чисел весьма сложна. На становление современной европейской (принятой
сейчас в большинстве стран мира) системы цифр большое влияние оказало развитие письменности.
Уровень математического знания уже в древних цивилизациях
был достаточно высок. Практические потребности везде вызвали освоение четырех действий
арифметики – сложения, вычитания, умножения и деления, а в некоторых регионах –
возведения в степень, извлечения корней, известны были и дроби. Очевидно, что эти
операции требовали определенной фиксации чисел. Понятия числа как такового в древности
не существовало[5],
скорее имелось наглядно-чувственное представление о тождестве количества объектов в различных группах однотипных
объектов, между которыми устанавливалось взаимнооднозначное соответствие (например,
между пальцами на руке и считаемыми предметами). Неудивительно поэтому, что у некоторых
народов в древности названия чисел задавались через название предметов, которые
всегда существуют в соответствующем количестве; так, например, в древней Индии единицу
можно было задать как «Солнце», «рот» и т.п.; двойку – как «уши», «глаза» и т.д.
В названии чисел в ряде языков имеются указания на род пересчитываемых объектов;
так, в Китае есть отдельные иероглифы для обозначения чисел мужского и женского
рода, латынь имеет три рода для числа один (unus, una, unum); аналогично в современном
русском языке есть три варианта слова «один» в зависимости от рода (один, одна,
одно) и два – для обозначения двух (два и две), тогда как для всех остальных названий
чисел такой дифференциации нет, имеют род и все порядковые числительные (пятый, пятая, пятое). Отметим, что названия
чисел, учитывающие род, препятствуют общему пересчету разнородных объектов. Это напоминает нам о некоторых этапах в эволюции
счета в целом: по-видимому, сначала пересчитывались не только однородные объекты,
но и объекты одного качества, т.е., например, к числу слив нельзя было добавить не только число корзин, но и число
груш, объекты каждого типа пересчитывались отдельно, причем числительные использовались
только в сочетании с именами пересчитываемых предметов. Арифметические операции
были операциями не с числами как таковыми, а именно с пересчитанными объектами определенного
типа. Вспомним, например, попытку Мальвины позаниматься с Буратино арифметикой в
сказке А.Н. Толстого «Золотой ключик, или Приключения Буратино». Мальвина говорит
Буратино: «– Предположим, что у вас в кармане два яблока. Некто взял у вас одно яблоко. Сколько у вас осталось яблок? – Два. … – Почему?
– Я
же не отдам Некту яблоко, хоть он дерись! То, как Буратино решал арифметическую задачу Мальвины,
является не просто шуткой, но и напоминанием о древнем этапе в развитии счета. Если
для Мальвины суть задачи – это операция на вычитание, яблоки взяты для примера,
то для Буратино важно, что это именно яблоки, которыми он не собирается ни с кем
делиться. Можно предположить, что в формировании все более абстрактных
представлений о числе – количестве объектов существенную роль сыграло то обстоятельство,
что разные группы объектов пересчитывались
с помощью одних и тех же предметов – пальцев,
палочек, камушков и т.п. Само появление в речи названий чисел произошло не сразу
и стало результатом длительного интеллектуального развития. Об этом же свидетельствует
и тот факт, что во многих языках мира названия чисел «один» и «два» существенно
отличаются от соответствующих числительных – «первый» и «второй», а вот для больших
(«три» – «третий», «четыре» – «четвертый» и т.д.) демонстрируют явную взаимосвязь.
Скорее всего причина лежит в том, что самый ранний счет имел вид: один, два, много.
Доводом в пользу этой точки зрения является и то, что во многих древних языках,
например древнегреческом, существовали три грамматические формы: единственное, двойственное
и множественное число. Важным этапом в развитии арифметики стало возникновение
различных систем счета, наиболее распространенными
были шестидесятеричной, пятеричная, десятеричная и комбинированная пятерично-десятеричная.
А вот майя в своем календаре использовали еще и двадцатеричную систему. Происхождение
трех последних не представляет никакой загадки и явно связано с количеством пальцев
на руках или руках и ногах, с шестидесятеричными дело обстоит несколько сложнее.
В основе месопотамской системы лежат числа 10 и 6. Шестерка же представляет собой
две тройки, и, по-видимому, именно тройка является здесь исходным числом. Но почему
опять тройка? Ответ на этот вопрос дает нам современная психология: три – это то наибольшее количество объектов,
которое фиксирует нетренированное сознание и которое без специальных усилий сразу
запоминается. И лишь немногим сложнее фиксация и запоминание двух троек. Посмотрите, например, на число,
заданное количеством палочек: ||||||. Чтобы понять, сколько их, их надо хотя бы
начать пересчитывать. А теперь бросьте взгляд на следующее: ||| |||. Здесь вы сразу
видите и понимаете, что это две тройки.
Аналогичный принцип используется и в настоящее время, например при записи номера
телефона, когда семизначное число записывают, разбивая на группы по две-три цифры.
Поэтому неудивительно, что шестидесятеричная система относится
к числу древнейших, например, такая была в Вавилоне. В ее основе лежали числа 1, 60, 600, 3600, она
и сейчас сохранилась при делении окружности, а также в организации трудовой деятельности
– в неделе, где шесть дней рабочих, а седьмой – выходной. Запись чисел осуществлялась
в шесть столбцов, в каждом десять рядов, таким образом, каждый новый столбец давал
число на порядок больше, чем предыдущий. Имелась шестидесятеричная система счета
и в древнем Китае, но там она использовалась в основном в календаре, что было связано
с выделением особого астрономического цикла, учитывающего время вращения Сатурна
(11,92 земного года, т.е. около 12). Здесь «опорными» числами были 12 и 5. Арифметические операции в древности обычно осуществлялись
практически-наглядным образом: счет велся с помощью пальцев и их аналогов – счетных
палочек, черточек или зарубок, а также камушков или узелков, графическими аналогами
камушков можно считать точки. О подсчетах с помощью пальцев или палочек говорит
и то, что во многих древних системах счета числа 1, 2, 3, а иногда и до 9 задавались
в виде соответствующего числа черточек – вертикальных (египетская, вавилонская,
греко-ионийская, римская и т.д.) или горизонтальных (китайская, майя). Имеются случаи
и комбинированного расположения; так, у протокельтов[6]есть вертикальные (с наклоном вправо и влево) и горизонтальные черточки. В этой последней пятеричной системе счета вертикальные
черточки с наклоном вправо / означали единицы, и их было максимум четыре ////, тогда
как черточки с наклоном влево \ обозначали пятерки, поэтому \\ значило десять и
т.д. Эти знаки представляют собой интересный вариант сочетания иконичности и условности.
Относительно их происхождения хотим высказать следующую гипотезу. Сами по себе черточки
– это явные подобия пальцев. Удобно расположите перед собой свою левую руку с ладонью
внутрь, и тогда четыре пальца (от указательного до мизинца) окажутся естественными
прообразами четырех черточек с наклоном
вправо, тогда как большой палец будет аналогом палочки с наклоном влево, и в силу своего особого положения
– нахождения на той же ладони, но в противопоставлении всем остальным пальцам, его
знак – черточка в наклоном влево – становится условным знаком, обозначающим всепальцы данной ладони. Точно такой же визуальный эффект дает нам и правая ладонь,
повернутая тыльной стороной наружу. Этот последний вариант расположения теперь уже
обеих ладоней позволяет понять и характер записи ряда больших чисел: соединим большие
пальцы обеих ладоней, и они образуют знак /\, означавший 6 (1+5), правая черта
(большой палец правой руки) оказывается здесь условным знаком всей пятерки пальцев
правой ладони, а левая (большой палец левой руки) – иконическим знаком одного отдельного
пальца левой ладони. Визуальное подобие //\ (7) – две ладони в том же положении,
но с указательным пальцем левой руки, отведенным в сторону большого, аналогично
для ///\ (8) и ////\ (9). А вот у записи 10 как \\ наглядного прообраза уже нет,
здесь степень условности возрастает. Максимальное число, которые записывалось таким образом,
– 29 (////\\\\\), т.е. число дней в лунном месяце. Связь с лунным календарем прослеживается
и в форме объектов, на которые чаще всего наносились такие символы, т.е. «серпов».
Впрочем, на объектах бронзового века, найденных рядом с «Полями погребальных урн»,
имеются и другие символы, которые пока не расшифрованы: это и строго вертикальные
или горизонтальные черточки | и – (от одной до четырех), «перевернутые» соединенные
черточки («галочки») – \/, причем тоже в наборе от одного до четырех –
\/\/\/\/, они же, но развернутые острием влево <, а также точки и другие знаки.
По-видимому, они служили для обозначения больших чисел, но каких именно, до сих
пор остается неясным в силу их чистой условности. Кстати, то, что арифметические операции обычно велись в древности с помощью вспомогательных предметов, перемещаемых с одного места на другое, объясняет, например, такие странные для современного человека названия математических операций, как «в квадрате» или «в кубе», возникшие в Древней Греции. Скажем, «три в квадрате» получалось следующим образом: в ряд выкладывались три камушка, под ними еще три, в затем еще один такой же ряд, в результате получался вполне наглядный квадрат: • • • • • • • • • «Практический» способ счета долгое время позволял людям обходиться
без полного набора специальных знаков чисел (цифр), хотя некоторые из них и получали
свое обозначение, что было существенно для фиксациичисел – как исходных, так и получаемых в результате соответствующей операции. Так,
в Древнем Египте, где сформировалась десятеричная система счета, использовались
особые знаки для чисел 1, 10, 100, 1000, 10 000, 100 000 и даже 1 000 000 (последнее обозначали фигуркой человека,
поднявшего руки в знак удивления). Учитывая масштабы строительства, которые велись
в этой стране, размеры египетской армии и т.п., использование таких больших чисел
было вызвано необходимостью. В Египте возникли и две довольно простые и удобные
системы записи чисел. В более древней из них (период Древнего царства) конкретное
число задавалось нужным количеством
повторений соответствующего знака, так, один обозначалась вертикальной черточкой│ («черта»), два – две такие черточки –
║, и так до 9. Для обозначения 10 использовался
особый иероглиф – Ո («пятка»), 20 – подряд два таких иероглифа и т.д.
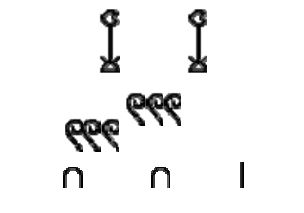
Так, например, число
36 записывалось как
или как
поскольку строго фиксированного направления
записи не существовало (и в этом не было никакой необходимости, так как уже по виду
знаков было ясно, к какому разряду они относятся. Могли числа записываться и вертикально,
например, 2621 как:
В современной системе записи это выглядело
бы как: 1000+1000+ 100+100+100+ +100+100+100+ 10+10+1 Основным неудобством данной системы было то, что при повторении
какого-то знака более трех раз их количество не воспринималось и не запоминалось
сразу, а значит, каждый раз их приходилось пересчитывать. Не случайно в приведенной
выше египетской «вертикальной» записи числа 2621 иероглифы, задающие число 60, разбиты
на две горизонтальные группы по три знака. Однако по мере развития культуры потребность в специальных
знаках для чисел росла, и здесь весьма существенную роль сыграло развитие письма:
во многих древних цивилизациях в качестве знаков для чисел стали использоваться
знаки письменности – соответственно, иероглифы, слоги, буквы. Почему те или конкретные
знаки письменности стали обозначать определенные числа, сейчас в большинстве случаев
уже невозможно установить. Интересную информацию такого рода дает нам изучение древнегреческой
культуры с ее алфавитным письмом. Пополнив финикийский алфавит гласными буквами
и создав тем самым полноценный алфавит, древние греки, по-видимому, стали первыми
и в обозначении чисел буквами. В Древней Греции (примерно с IX в. до н.э.) сначала употребляли
аттическую систему записи, где цифрам соответствовала первая буква слова, которым
называлось данное число (единственное
исключение имело место для иос – 1, обозначавшейся вертикальной чертой, где само
начертание буквы было похоже на палец
или имитирующую его черту или зарубку), т.е., например, для современного русского
языка это выглядело бы следующим образом: один
– О, пять – П, десять – Д и т.д. Но эти специальные знаки имелись далеко не для всех чисел,
а только для 1 (иос – И), 10 (дека – Д), 100 (гекатон – Г), 1000 (хилиой
– Х), 10 000 (мюриой – М), а кроме того,
для 5 (сначала это была буква генте
– Г, а затем она трансформировалась в
пенте – П). А еще имелись особые сочетания знака 5 – Г/П и знаков, кратных
10, которые ставились внутри Г/П, что позволяло записывать 50, 500,
5000 и 50000. Все «промежуточные» числа, не имевших специальных обозначающих их
знаков, записывались методом повтора имеющихся знаков; так, 23 – ДДИИИ
(10+10+1+1+1), т.е. здесь имел место принцип повторения, как и в Египте, но повторяться
знак мог только четыре раза. Числа записывались слева направо, причем в записи шли
сначала числа большего разряда, а затем меньшего. Эта система записи не позволяла
оперировать с очень большими числами, но, по-видимому, в них и не было особой необходимости.
С семиотической точки зрения эта система записи чисел интересна несколькими особенностями.
Во-первых, само наличие особых имен (названий)
для хотя бы некоторых чисел уже свидетельствует о становлении представления о числе
как таковом (абстрагирующееся от конкретных пересчитываемых объектов), а значит,
и применяемом к множеству любых объектов
соответствующего количества. Во-вторых, здесь имеет место не просто фиксация имени числа в речи, а запись этого имени. В-третьих, на смену полному
записанному имени приходит его первая буква, которая становится знаком данного имени
и благодаря этому и знаком числа. В-четвертых, здесь сливаются буквы и цифры, и
слово получает числовое значение, создавая предпосылки для нумерологии. Для того
чтобы отличать запись числа от слова, состоящего из тех же букв, использовались
специальные знаки – черточки (титло) над буквами или знак кавычки в правом верхнем
углу, работавшие как «переключатель» на клавиатуре компьютера, обеспечивая переход
от букв к цифрам. Очень важным свидетельством того, что в середине I тыс. до н.э.
у древних греков существовало уже представление о числах как таковых, а не просто
количестве пересчитываемых объектов, является тот факт, что в пифагореизме числа
провозглашаются первоосновой бытия, а у Платона в царстве идей имеются идеи
чисел. Примерно с III в. до н.э. аттическая система записи сменилась
на ионийскую (новогреческую), где буквы стали обозначать число по принципу их порядкового места в алфавите, т.е. опять-таки,
на примере современного русского алфавита: а – 1, б – 2, …, й – 10, …, т – 100,
ь – 1000 и т.д. Здесь появляются графические знаки для чисел – «протоцифры» (и опять-таки,
чтобы отличить их в этом использовании от собственно букв, над ними или рядом с
ними ставились особые знаки – детерминативы). Одним из неожиданных последствий применения
ионийской системы стало быстрое упорядочение алфавита, т.е. фиксируется обратное
влияние системы записи чисел на письменность. Чтобы доводить счет до девяти сотен,
в ионийской системе записи использовалось еще и несколько букв доклассической письменности,
всего их оказывалось 29 (что опять напоминает нам о лунном календаре). При ионийской
записи самое большое число, которое этим методом могло быть записано (без повтора
какой либо буквы), было 999. Эта древняя «оцифровка» алфавита – отождествление букв и знаков
чисел – получила широкое распространение у многих народов Средиземноморья, использующих
алфавитное письмо, в частности и у древних евреев. В каббале вообще было провозглашено
тождество «трех серафимов» – числа, звука и буквы, что породило такой мистический
прием нумерологии, как гематрию, где любое слово (чаще всего – имя собственное)
получало числовое значение (сумма чисел, соответствующих буквам, составляющим данное
слово). Так, с использованием современного русского алфавита, например, слово «благо»
будет иметь значение: 2 (б) + 40 (л) + 1
(а) + 4 (г) + 60 (о) = 107. А вот слово «зло» имеет значение: 8 (з) + 40 (л) + 60 (о) = 108. Все слова с одним
числовым значением считались внутренне взаимосвязанными и по значению, т.е. любой
объект такого рода будет считаться благим или злым. Наиболее известный в европейской
культуре пример использования гематрии – это Число зверя – 666, приведенное в Апокалипсисе
и получившее разнообразные расшифровки. У других народов были и иные способы записи чисел. Дошедшей
из древности до наших дней и все еще иногда используемой в особых случаях является
римская цифра, свидетельствуя о глубоком влиянии римской культуры на европейскую.
Так, в современном русском языке римские цифры используются в печатных и рукописных
текстах для обозначения тысячелетий и веков (II тыс. до н.э., I в. н.э. и т.п.),
а в рукописных еще в ХХ в. они употреблялись и для обозначения месяцев
(7.V.1998); употребляются римские цифры во всем мире и на циферблатах часов. Принято считать, что римляне позаимствовали свою систему
записи чисел у этрусков, но откуда ее взяли сами этруски, остается не вполне ясным:
одни ученые считают, что у протокельтов, другие же указывают на ее явное сходство
с аттической системой восточных греков, и эта точка зрения представляется нам более
убедительной. Ведь в I тыс. до н.э. на юге Апеннинского полуострова и близлежащих
островах было много греческих поселений, и возможность влияния греков на этрусков
несомненна: так, письменность этрусков развивалась под влиянием греческого письма.
Кроме того, римская система повторяет некоторые важнейшие принципы аттической системы,
которые не видны у протокельтов: числа 100 – centum и 1000 – mille обозначаются
соответственно буквами С и М. Появление знака D для 500, возможно, имеет еще более
удивительное происхождение. Дело в том, что ранее римляне иногда половину числа обозначали половинкой знака вдвое большего числа. А
древнейшим обозначением тысячи был кружок, перечеркнутый одной или двумя вертикальными
линиями, и его правая половина похожа
по начертанию на букву D. Что же касается знаков I, V и X, начертанием похожих на
протокельтские, то это внешнее сходство мало что доказывает. Вертикальная черточка
– это широко распространенное обозначение числа один, так же как и ее повторение
для обозначения 2–4, и у римлян, в отличие от протокельтов, она не наклонная. Особый
знак для пяти, связанный с пятеричным счетом, имеет место и в аттической системе. И у римлян он отличается от протокельтского
(\), а что у протокельтов значило \/ (как и Х) – до сих пор неизвестно. Более естественное
объяснение римского знака для пяти другое, опять несущее явные следы счета на пальцах:
так, | (1), || (2), ||| (3), |||| (4) – это просто количество пальцев на руке, противостоящих
большому, тогда как V – стилизованное изображение раскрытой ладони, а Х – двух скрещенных
рук, т.е. 10 пальцев (протокельтское обозначение десяти – \\). Сходство в начертаниях позднее привело к
тому, что эти три римские цифры стали писаться как буквы латинского алфавита – I, V, X (и в таком качестве они могут использоваться
на клавиатуре компьютера), хотя ни с принципом аттической, ни ионийской записи это
не имеет непосредственной связи. Скорее здесь сработал сам принцип сближения начертания
букв и цифр. Знаки для 6, 7, 8, 9, 11 и т.д. являются у римлян «вторичными»,
комбинациями «основных», где не допускается подряд четырех и более использований
одного и того же знака (кроме единицы[7]).
Если во всех вышеназванных системах при записи чисел использовался только принцип
сложения (путем повтора знаков), то у римлян уже применяется и вычитание: знак слева
(только один) означает вычитание из «основного» числа, а такой же знак справа –
добавление (до трех), поэтому IХ – это 9 (10–1), а ХI – это 11 (10+1), ХС – это
90 (100–10), СХХ – 120 (100+10+10) и т.д. При записи больших чисел используется
позиционный принцип: крайние справа – наименьшего разряда, левее – большего на порядок,
еще левее – еще больше на порядок (например, сотни-десятки-единицы) и т.д. Считать
в письменном виде так записанные числа было крайне сложно, но это мало кого смущало,
поскольку все реальные операции с числами велись с помощью счетной доски (абака).
Римская счетная доска, как и греческая, была «пятерично-десятеричной»: она вертикально
делилась на две части, в левой части было пять «косточек», а в правой – две, что
позволяло слева фиксировать числа от 1 до 5, а справа – одну или две пятерки. Принципиальный прорыв в становлении системы цифр был совершен
в Древней Индии, где, по-видимому, уже к V в. до н.э. сложилась система записи чисел,
которая и легла в основу современной. Ее важнейшими отличиями являются: понятие
«нуля» (шунья – ничто, пустота) и специальный знак для него – 0; наличие специальных
знаков (цифр) для всех чисел от 1 до 9 и запись любых чисел только с их помощью,
с использованием нуля + нуля; строгая позиционная система записи. Специальные знаки для обозначения чисел от 1 до 9 появлялись
и в других местах, в частности они присутствуют уже в ионийской системе древних
греков. Роднит их и то, что в Индии знаки цифр возникли на базе письменности (из
знаков слогового письма брахми; начертания индийских цифр, с которыми познакомились
в эпоху Средневековья арабы, были связаны с более поздним письмом деванагари). Возникали
в других регионах и хотя бы отдельные элементы позиционной системы. Что же касается
индийского понятия «нуля», то можно говорить лишь о некоторых его аналогах в других
регионах; так, в вавилонской шестидесятеричной системе записи, строящейся как шесть
столбцов по 10 строчек в каждом, некоторым аналогом нуля можно считать пустой столбец.
Само введение понятия нуля, понимаемого как пустота, небытие, ничто, отсутствие
(кстати, его древнейшим названием было, по-видимому, санкскритское слово «дыра»,
а обозначался ноль как кружок), свидетельствовало об очень высоком уровне абстрактного
мышления. Ведь представления о числах родились из пересчета объектов, а если нам
нечего пересчитывать, то и откуда взяться представлению о нуле? Напомним, что и
в древнейших космогонических мифах мир никогда не возникает и не создается из «ничего»:
Космос, т.е. «Порядок», появляется как результат упорядочения материального Хаоса.
Примерно в то же самое время, т.е. в середине I тыс. до
н.э., проблема пустоты-небытия стала объектом исследования и в древнегреческой философии.
Она обсуждалась у Парменида и у Левкиппа.
У Левкиппа понятие пустоты относится к чувственно воспринимаемому миру и
появляется как понятие пустого пространства, в котором существуют и перемещаются
атомы и объекты, состоящие из атомов (в дальнейшем это же понятие используется у
всех атомистов). У Парменида же в его поэме «О природе» подробно анализируется более
общая философская проблема бытия небытия,
но обсуждается она для истинного умопостигаемого бытия, а не чувственно воспринимаемого
мира. И Парменид приходит к выводу, что небытие скорее не существует, нежели существует.
По-видимому, его вывод разделялся многими другими греческими философами, поскольку
эта проблема в дальнейшем не обсуждалась широко. В Индии же понятие «небытия» связывалось с чувственно воспринимаемым
миром и играло важную роль в различных философских системах. В школе вайшешика различалось
даже четыре вида небытия. Для любого объекта, например глиняного кувшина, необходимо
было учитывать и связанные с ним виды небытия:
1) до возникновения этого кувшина;
2) после его разрушения; 3) во время его
существования как отсутствие у него каких-то
свойств, например мягкости; и 4) как нетождественность другим объектам, например
бытие данного объекта как кувшина есть его небытие как ткани, меча и т.д. В дальнейшем
понятие «небытие» нашло свое развитие в буддизме, а в эпоху Средневековья и в веданте.
Поэтому не приходится удивляться тому, что именно в Индии додумались до понятия
«нуля» и его практического использования в математике. Когда арабы впервые познакомились с индийской системой
записи, точно не известно. Но в ее популяризации во всем арабском мире большую роль
сыграл известный ученый Аль-Хорезми (ок.
783 – ок. 850), написавший книгу «Об индийском счете», он же, по-видимому, первый
использовал знак нуля. На арабском языке ноль стал называться «цифр» (ничего, пустота),
откуда и произошло латинское слово «cifra», фонетической калькой которого является
русское слово «цифра». Книга Аль-Хорезми стала широко известна во всем мусульманском
мире, в том числе и в Испании. Благодаря связям между мусульманской Кордовой и христианской
Барселоной в нее поступали сообщения о многих научных достижениях мусульманского
мира. Одним из первых христиан, познакомившихся с данной книгой, был ученый монах
Герберт Орильякский (ок. 946 – 1003), позднее ставший папой римским под именем Сильвестр
II. Герберт сразу оценил преимущества данной системы и много сделал для ее популяризации.
В ХII в. книга Аль-Хорезми, хотя и не полностью, была переведена на латинский язык
под названием «Algoritmi de numero Indorum». И только в этом переводе книга и дошла
до наших дней, так как арабоязычный вариант не сохранился. В первоначальном варианте цифры у арабов (в том числе
в данном сочинении) имели совсем другое начертание – далекое как от современного,
так и от индийского, но близкое к буквамарабской письменности. Существует интересная легенда о том, откуда взялось современное
начертание «арабских цифр», резко расходящихся в начертаниях с буквами, в частности,
об этом рассказано в (Cajori, 2007). В этих новых цифрах количество углов соответствовало
числовому значению: в нуле, изображавшемся кружочком, углов вообще нет, в единице
(она изображалась как ┐) – один угол, в восьми – их восемь и т.д. Таким образом,
в начертании этих искусственно созданных графических знаков – цифр – возродилась
исходная иконичность. Со временем, когда употребление этих цифр стало привычным,
их начертания стали изменяться – «закругляться», что, скорее всего, было связано
с развитием скорописи. И новые арабские цифры из иконических превратились в
чисто условные знаки. Любопытно, что в ХХ в. исходное «угловое» начертание цифр
в какой-то степени возродилось в стандарте почтовых индексов, но только для единицы
и восьмерки – причем скорее всего случайно – сохранился принцип соответствия числа
углов и числового значения. В Европе арабские цифры сначала применяли только в университетах,
и далеко не все одобряли их использование: так, во Флоренции в 1299 г. даже был
издан закон, запрещающий их употребление. Тем не менее итальянские купцы, для которых
жизненно важно было иметь удобную и простую систему записи чисел и операций с ними,
стали ее широко применять, и к ХVI в. уже почти вся Европа перешла с римских на
арабские цифры, их стали применять на монетах[8],
для нумерации станиц книг[9]и т.д. Тот факт, что арабские цифры ведут свое происхождение
из Индии, получил признание в Европе только в XIX в. Первым, кто пришел к такому
выводу, был русский востоковед Г.Я. Кер (1692– 1740), служивший переводчиком в Москве
в коллегии иностранных дел. В настоящее время любой образованный человек хорошо
знает, что арабские цифры на самом деле являются индийскими. Хотя, учитывая происхождение
самого начертания цифр, следует уточнить, что все арабские цифры, кроме нуля, и
на самом деле являются арабскими, но возникшими на базе индийских. Введение арабских цифр и позиционной системы записи произвело
революцию, потому что упростило запись чисел и дало возможность записывать любое
(сколь угодно большое) число, это позволило также выработать алгоритм для производства
всех арифметических действий в письменном виде – без помощи счетной доски (абака).
Тем не менее вплоть до XVIII в. абак продолжал применяться в Европе, а несколько
предшествующих столетий были временем ожесточенной борьбы между «абацистами» и «алгоритмиками».
На смену абаку пришли механические счетные машины: с XVII в. ведется активная работа
по созданию механических арифмометров (в 1642 г. Блез Паскаль изобрел «паскалину»,
в 1672 г. Лейбниц создал свой калькулятор и т.д.), серийный выпуск арифмометров
начался в 1820 г. (Тома де Кольмар). В середине ХХ в. широкое распространение получают
электромеханические арифмометры, а в начале 1980-х годов электронные калькуляторы
полностью вытесняют механические. Таким образом, вычисления в письменном виде опять
оказались практически ненужными, заменяясь на «внешние действия». Возвращаясь к вопросу о связи букв и цифр, отметим, что
к настоящему времени она оказалась практически полностью разорванной, о чем свидетельствует,
например, клавиатура компьютера с ее отдельными клавишами для цифр и букв. А вот
клавиши мобильника с совмещением букв и цифр напоминают об ионийском принципе записи.
Напоминанием об этой связи остается и использование ряда латинских букв в качестве
римских цифр, и равноправное применение как цифр, так и букв (в их алфавитном порядке)
в нумерации пунктов при перечислении. Список литературы 1. Ассман Я. Египет: Теология и благочестие ранней
цивилизации. – М.: Присцельс, 1999. – 368 с. 2. Гриненко Г.В. Сакральные тексты и сакральная коммуникация.
– М.: Новый век, 2000. – 444 с. 3. Леви-Брюль Л. Сверхъестественное в первобытном мышлении.
– М.: Педагогика-Пресс, 1994. – 605 с. 4. Моррис Ч. Основания теории знаков // Семиотика.
– М.: Радуга, 1983. – С. 37–89. 5. Сираждинов С.Х., Матвиевская Г.П. ал-хорезми
– выдающийся математик и астроном Средневековья. – М.: Просвещение, 1983. – 79
c. 6. Cajori F. A history of mathematical notations. – New York: Cosimo, 2007. – Vol. 1. – 472 p.
[1] Ч. Пирс – родоначальник семиотики – выделял три основных типа знаков: иконические, индексы и условные знаки. Иконические знаки характеризуются тем, что означающее обладает объективно существующим сходством с означаемым, у индексов означающее и означаемое связаны причинно-следственной связью, условные знаки предполагают чисто договорный характер отношения означающего и означаемого (Ч. Пирс эти последние знаки называл «символами», но мы предпочитаем этот термин не использовать, так как он имеет множество культурных коннотаций). [2] Интересны в этом смысле некоторые средневековые произведения (византийские и древнерусские иконы, иранская классическая миниатюра), где на одном поле изображены близкие по времени, но все-таки не одновременные события, происходящие в одном месте. Но в них никогда не выстраивается графически «последовательность» событий, они все оказываются «одновременными». [3] Интересно отметить, что такой же принцип используется и в современных азбуках, где рядом с изображением буквы рисуется объект, имя которого начинается с той же буквы, облегчая детям ее запоминание. [4] Подробнее эта проблема рассматривается в (Гриненко, 2000). [5] Как ни парадоксально, отсутствие
в математике понятия «числа» обнаружил только в XIX в. немецкий математик Георг
Кантор, который и разработал теорию множеств специально для того, чтобы дать такое
определение. [6] Символы полей погребальных
урн – «серпы» и другие объекты (по-видимому, ритуального назначения), которые были
обнаружены в окрестностях Заале. Относятся примерно к периоду 1500–1250 гг. до н.э.
[7] Знак IV для обозначения четырех
стал регулярно использоваться только с XIX в., а вот на циферблате многих часов
для обозначения четырех до сих пор сохраняется знак «IIII», правда, это делается
скорее из эстетических соображений – для симметрии со знаком VIII. В древнеримском
календаре «parapegma» III–IV вв. н.э. мы встречаемся с тем, что используется четырехкратное повторение
символа I при написании не только числа 4, но и 9, 14, 24 и 29. [8] В России первая чеканке монет
с арабскими цифрами была осуществлена в 1654 г., а последний раз славянские цифры
использовались на монетах 1718 г. [9] Известно, например, что нумерация страниц индийскими цифрами в книге Петрарки была впервые дана в 1479 г.
Публиковалось: Человек: Образ и сущность. Гуманитарные аспекты: Ежегодник / РАН. ИНИОН. – М., 2016: Информационный универсум и самосознание современного человека. Стр. 200-224 | |||||||||
28.02.2021 г. | |||||||||
Наверх | |||||||||



 Культуролог в ЖЖ
Культуролог в ЖЖ  Культуролог в ВК
Культуролог в ВК